Linux E X P R E S

V úvodu příspěvku je nastíněna současná situace stavu připravenosti Fakulty managementu a ekonomiky Univerzity Tomáše Bati ve Zlíně (FaME UTB) na distanční formu vzdělávání. Nedílnou součástí distančního vzdělávání je samostudium, a proto je příspěvek zaměřen na využitelnost programu WinQSB při výuce předmětu Kvantitativní metody v rozhodování. Použití programu je demonstrováno na příkladu případové studie. Program WinQSB sice nepatří formálně do kategorie open source software, spíš bychom jej zařadili mezi freeware, jehož vývoj, zdá se, byl pozastaven. I tak program prokazuje svou důležitost ve výuce na naší fakultě.

Zkušenosti s výukou předmětu Kvantitativní metody v rozhodování

V příspěvku jsou na ukázce řešené případové studie zhodnoceny zkušenosti s využíváním programu WinQSB (zip) ve výuce předmětu Kvantitativní metody v rozhodování. FaME UTB ve Zlíně nemá zatím akreditováno distanční vzdělávání, ale kurzy DiV, které absolvují někteří pedagogové, jsou předzvěstí trendu, kterým se fakulta hodlá ubírat. Byla zakoupena také licence pro výukový program EDEN (což je prostředí pro tvorbu distančních textů). V rámci rozvojového programu bylo zahájeno zpracování výukových a studijních materiálů v prostředí Moodle. Jedná se o disciplíny, které jsou součástí kombinovaného studijního programu. Využívání systému Moodle je plánováno i na dalších fakultách UTB ve Zlíně.

Disciplína Kvantitativní metody v rozhodování se v současné době vyučuje v prezenční formě studia i v kombinované formě studia ve všech studijních programech akreditovaných na FaME UTB ve Zlíně v magisterském studiu (1. ročník magisterského programu). Kombinovaná forma studia vychází z učebního plánu studia prezenčního. Vykazuje již řadu distančních prvků, zejména uplatňovaných v kombinované formě studia (použití programu WinQSB, Microsoft Project, pomocí nichž si studenti ověřují správnost sestavení matematických modelů...). Nezbytná je také možnost komunikace s vyučujícím přes Internet.

Každý pedagog, který vyučuje v kombinované formě studia, je nucen těmto studentům poskytnout speciální studijní materiály, které jim umožní samostudium. Ne každá problematika se dá jednoduše studovat distančně. V kurzu Kvantitativní metody v rozhodování jsou řešeny případové studie z praxe. Studenti musí na základě rozboru ekonomického problému sestavit matematický model. Ruční řešení tohoto modelu je pro složitost výpočtu a časovou náročnost téměř nemožné a v dnešní době informačních technologií i velmi neefektivní.

Naše fakulta využívá speciální výukový program WinQSB (verze 1.00 pro Microsoft Windows), který je i volně stažitelný na Internetu. Obsahuje nejen moduly pro řešení úloh lineárního programování, ale i moduly z ostatních oblastí operačního výzkumu podle tohoto členění:

• Analýza rozhodování (Decision Analysis)

• Dynamické programování (Dynaming Programming)

• Plánování výrobních zdrojů (Facility Location and Layout)

• Předpovědi a lineární regrese (Forecasting and Linear Regression)

• Lineární programování (Linear and Integer Programming)

• Analýza Markovových procesů (Markov Process)

• Plánování materiálových zdrojů (Material Requirements Planning)

• Síťová analýza (Network Modeling)

• Nelineární programování (Nonlinear Programming)

• Analýza PERT_CPM

• Kontrola kvality (Quality Control Chart)

• Rozvrhování pracovních úkolů (Job Scheduling)

• Teorie front (Queuing Analysis)

• Modely hromadné obsluhy (Queuing System Simulation)

Práce s tímto programem je jednoduchá a na veškeré nejasnosti lze najít odpověď v nabídce Help. Bez použití specializovaného programu by výuka tohoto předmětu byla pouhou ukázkou „zboží přes sklo výlohy bez možnosti vyzkoušet si kvalitu a funkčnost“.

Využití tohoto programu ve výuce je doloženo ukázkou vyřešené případové studie. Je z tématického celku: Lineární programování – sestavování matematických modelů – kapacitní úlohy.

Snad tato ukázka bude přínosná i pro ostatní pedagogy a čtenáře openMagazinu, kteří se zabývají operačním výzkumem (matematickou optimalizací, simulacemi atp.).

Případová studie: Plán rozšíření výroby pro firmu vyrábějící hračky

Podnikatelské prostředí: výrobní firma.

Firma byla velmi úspěšná během prvních šesti měsíců působení a nyní hledá možnost přesunutí výroby do oblasti, kde výdaje na práci a materiál jsou podstatně levnější. Podařilo se jí nalézt oblast, kde je levná pracovní síla a uzavřít zde smlouvu s místním dodavatelem plastů. Dodavatel se zavázal zásobovat firmu 1500 kg plastů týdně, za podstatně nižší ceny. Výroba by měla být efektivnější, došlo by k zdvojnásobení zisku z výroby V1 až na 480 Kč/kus a k ztrojnásobení zisku z výroby V2 až na 450 Kč/kus.

Nové prostory by byly vybaveny stroji a dělníky pracujícími čtyřicet hodin v řádné pracovní době a navíc dělníci mohou odpracovat týdně třicet dva přesčasových hodin.

Z účetního hlediska vybavení pro dělníky, sociálního pojištění, zdravotního pojištění, mzdy a provozních výdajů za jednu přesčasovou hodinu budou stát společnost o 5400 Kč více než jedna řádná hodina pracovní doby.

Firma udělala marketingový průzkum trhu i pro dva nové produkty V3 a V4, které by chtěla uvést na trh. V tabulce jsou uvedeny požadavky na materiál, čas a zisk z jednotlivých druhů výrobků.

Výrobek	Spotřeba plastů (kg/kus)	Spotřeba času (min/kus)	Předpokládaný zisk (Kč/kus, eur/kus)
V1	1	3	480, (15)
V2	0,5	4	440, (14)
V3	1,5	5	600, (19)
V4	2	6	660, (21)
Disponibilní množství	1500 kg	40 h řádná pracovní doba, 32 h přesčasová pracovní doba

Firma podepsala smlouvu s odběratelskou firmou na dodávku 240 ks výrobků V2 týdně. Marketingové oddělení provedlo průzkum trhu a na základě tohoto průzkumu rozhodlo, že nejoblíbenější výrobek V1 bude zahrnovat padesát procent celkové produkce a ostatní výrobky budou zahrnovat méně než čtyřicet procent produkce každý týden. Pod vlivem příznivých podmínek pro výrobu a odbyt oddělení vývoje navrhuje zvýšit celkovou výrobu hraček na tisíc kusů týdně.

Management firmy chce určit týdenní plán produkce hraček za změněných podmínek (včetně všech přesčasových hodin, pokud jsou nezbytně nutné). Cílem je maximalizovat týdenní zisk.

Rozbor problému

1. Firma chce maximalizovat čistý týdenní zisk.

2. Musí být stanoven týdenní výrobní plán jednotlivých výrobků.

3. Existují následující omezení:

   • dostupnost suroviny (plastů) – 1500 kg týdně,

   • řádná pracovní doba dělníků (40*60 = 2400 min týdně),

   • dostupnost přesčasové doby (32 h týdně),

   • minimální množství vyrobených V2 týdně (240 ks týdně),

   • vhodný výrobkový mix (V1 = 50 % z celkové produkce, V2, V3, V4 <= 40 % z celkové produkce),

   • minimální celková produkce (V1+V2+V3+V4 = 1000 ks).

Proměnné

Firma musí rozhodnout nejen o velikosti týdenní produkce jednotlivých výrobků, ale také určit výši přesčasových hodin týdně. To budou naše proměnné (neznámé).

x₁ = počet ks výrobků V1, vyráběných za 1 týden,

x₂ = počet ks výrobků V2, vyráběných za 1 týden,

x₃ = počet ks výrobků V3, vyráběných za 1 týden,

x₄ = počet ks výrobků V4, vyráběných za 1 týden,

x₅ = počet přesčasových hodin za 1 týden.

Účelová funkce

Chceme maximalizovat čistý týdenní zisk, účelová funkce je:

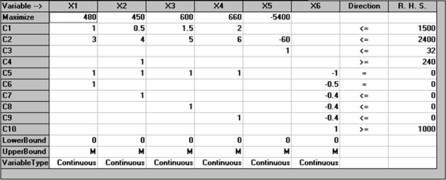
z_max = 480x₁+450x₂+600x₃+660x₄-5400x₅

Omezení

Omezení jsou následující:

1. Surovina (kg): x₁+0,5x₂+1,5x₃+2x₄ <=1500

2. Čas (min): 3x₁+4x₂+5x₃+6x₄ <=2400+60x₅

3. Přesčas (hod.): x₅ <=32

4. Požadavky odběratele V2 (ks): x₂ >=2400

Nyní musíme zavést další proměnnou x₆ = celková týdenní produkce (v ks)

5. Potom platí: x₆=x₁+x₂+x₃+x₄

Po úpravě: x₁+x₂+x₃+x₄-x₆=0

6. Týdenní výroba V1 = 50 % z celkové produkce: x₁=0,5x₆

7. Týdenní výroba V2 <= 40 % z celkové produkce: x₂ <= 0,4x₆

8. Týdenní výroba V3 <= 40 % z celkové produkce: x₃ <= 0,4x₆

9. Týdenní výroba V4 <= 40 % z celkové produkce: x₄ <= 0,4x₆

10. Celková produkce >= 1 000 ks týdně: x₆ >= 1000

Podmínka nezápornosti

Podmínka nezápornosti, tj. zajištění, že produkce nebude záporná, se dá vyjádřit:

x_i >=0, i=1,2,...,6

Řešení ve WinQSB

Vybereme si modul Linear and Integer Programming.

Volíme z menu File, poté New Problem. Po vyplnění dáváme OK.

Zadávání vstupních údajů do programu WinQSB

Po zadání všech údajů (pozor na užití desetinných teček) a nastavení nerovností (dvojklik na dané buňce) vybereme z menu Solve and Analyze, poté Solve the Problem.

Řešení problému pomocí programu WinQSB

Na následujících řádcích si výsledky okomentujeme.

Ekonomická interpretace problému

Řešení primárního problému

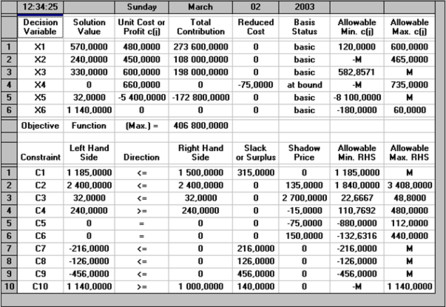
Optimální bude vyrábět týdně:

570 ks výrobků V1,

240 ks výrobků V2,

330 ks výrobků V3,

výrobky V4 vůbec nevyrábět,

při této skladbě výroby bude počet přesčasových hodin týdně 32 a celková týdenní produkce bude 1140 ks výrobků týdně.

Čistý týdenní zisk bude činit 406800 Kč (12712,5 eur).

Řešení duálního problému

Neméně důležité je i řešení duálního problému:

1. K dispozici máme 1500 kg suroviny, spotřebujeme jí při výše uvedené výrobě pouze 1185 kg. Zbytek 315 kg nám zůstane na skladě. Proto je zde stínová cena nulová.

2. Máme k dispozici 2400 min řádného pracovního času, který je plně využit. Přidáním jedné minuty řádného času do daného výrobního procesu by se hodnota čistého týdenního zisku zvýšila o 135 Kč = 4,2 eur. (Pro zvážení této eventuality je podstatné, kolik korun nás stojí jedna minuta řádné pracovní doby – tzn. mzdové a provozní náklady. Pokud je to částka nižší než 135 Kč, stojí za to uvažovat o rozšíření výroby, za předpokladu, že ostatní ukazatele jsou také příznivé.)

3. Máme k dispozici 32 hodin přesčasového pracovního času, který je plně využit. Stínová cena je 2700 Kč = 84,4 eur – tzn. přidáním jedné přesčasové hodiny do do daného výrobního procesu by se hodnota čistého týdenního zisku zvýšila o 2700 Kč. Platí zde podobná úvaha jako v předešlém bodě.

4. Máme vyrobit 240 ks výrobků V2, které vyrobíme. Vyrobením 1 ks výrobku V2 navíc by se snížil týdenní zisk o 15 Kč = 0,7 eur.

5. Pokud bychom zvýšili počet vyrobených výrobků o 1 ks týdně, snížil by se týdenní zisk o 75 Kč = 2,3 eur.

6. Máme vyrobit 570 ks výrobků V1, které vyrobíme. Vyrobením 1 ks výrobku V1 navíc by se zvýšil týdenní zisk o 150 Kč = 4,7 eur. Uvažovat o zvýšení výroby V1 je možné, pouze za předpokladu, že výrobní náklady na tento výrobek jsou nižší než 150 Kč/kus a všechny potřebné suroviny máme k dispozici v dostatečném množství.

7. Máme vyrobit alespoň 456 ks výrobků V2, vyrobíme jich o 216 ks více. Zde je stínová cena nulová, protože nemá smysl uvažovat o změně výše týdenního zisku, vyrobíme-li 1 ks V1 navíc. Totéž platí i o omezeních C8 až C10.

Literatura

1. Jablonský, J. Operační výzkum – kvantitativní modely pro ekonomické rozhodování. 1. vydání. Praha: Professional Publishing, 2002. 323 s. ISBN 80-86419-23-1.

2. Lawrence, J., Pasternack, B. Applied Management Science. New York: John Wiley, 1998. 665 s. ISBN 0-471-13776-6.

3. Gros, I. Kvantitativní metody v manažerském rozhodování. 1. vydání. Praha, Grada publishing, a.s., 2003. 432 s. ISBN 80-247-0421-8.

4. WinQSB (verze pro Microsoft Windows). Version 1.00. Copyright Yih-Long Chang. Ke stažení na webových stránkách kurzu. [online 2011-06-01]