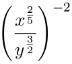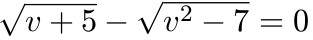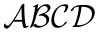LaTeX: Vytvoření písemky z matematiky

Trocha motivace úvodem

LaTeX je nadstavba TeXu, což je systém umožňující profesionální sazbu především matematických a technických knih. To byla ta dobrá zpráva, ta špatná (pro některé uživatele) je ta, že se jedná o sadu maker, které psány v čistě textové podobě provedou požadované vysázení textu do pěkné knižní sazby. Jinými slovy, LaTeX je nevizuální, tzn. psát můžete ve svém oblíbeném textovém editoru a výsledek uvidíte až v okamžiku, kdy si necháte zdrojový soubor vysázet LaTeXem.

Samozřejmě existují také vizuální editory, které vám usnadní proces zadávání různých značek do textu. Jedním z nich je např. populární LyX.

Na druhou stranu, pokud jste se někdy setkali s nevizuálním způsobem vytváření něčeho, buď jste si to oblíbili, nebo prokleli. Já patřím k té první skupině uživatelů, a tak mi to nedělá problém. Výhoda nevizuálního editoru spočívá přinejmenším v tom, že se při psaní textu jednoduše netrápíte tím, jak bude vypadat výsledek. Proč? Protože výsledek uvidíte teprve až po jeho vysázení. ;-)

Co budete potřebovat? Funkční instalaci LaTeXu. Na Debian GNU/Linuxu to představuje balíček texlive a texlive-lang-czechslovak. Možná ještě několik dalších, ale to poznáte až v průběhu práce s programem. LaTeX není žádný drobek, a tak se svou velikostí vyrovná ostatním "kancelářským" programům, které si ostatně také servítky neberou.

Jakmile máte připravený zdrojový soubor (viz dále), provedete jeho převod (vysázení) do běžně používaného formátu PDF takto:

pdfcslatex jméno_souboru.tex

Pozor! V systému se také nachází nástroj pdflatex, který provádí to samé. Tento nástroj ovšem nepodporuje češtinu!

Výsledkem předchozího příkazu je soubor jméno_souboru.pdf. Pokud se však příkaz v nějakém bodu překladu zdrojového souboru zastaví, např. z důvodu syntaktické chyby, bude potřeba chybu nejprve odstranit a pak provést překlad do formátu PDF znovu. To bylo ve zkratce a doslova z rychlíku to nejdůležitější, co je k úspěšné práci s LaTeXem třeba. Pojďme se nyní rovnou podívat na zdrojový soubor.

Zdrojový soubor

Pro ukázku bude sloužit mnou vytvořený soubor, který používám při vytváření čtvrtletních písemek z matematiky. Soubor může na první pohled působit poněkud složitě (zejména pro začátečníka) a až příliš jednoduše pro pokročilého uživatele LaTeXu. Je však pravdou, že jsem ho vytvářel a vylepšoval postupně a také platí, že mi jako šablona slouží pro vytváření dalších a dalších písemek. Jinými slovy, pokud si dáte se šablonou trochu práce, v budoucnu se vám za to odmění rychlostí a jednoduchostí, s jakou budete písemné práce připravovat.

Ukázkový soubor písemka.tex si můžete stáhnout. Jeho vysázení do formátu PDF provedete pomocí výše zmiňovaného nástroje pdfcslatex, PDF soubor si můžete stáhnout také.

Písemka z matematiky

Pojďme se nyní podívat na jednotlivé části:

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\documentclass[a4paper,11pt]{article}
\usepackage{ucs,czech}
\usepackage[utf8x]{inputenc}
\usepackage{amsmath}
\usepackage{amssymb}
\setlength{\topmargin}{-1in}
\setlength{\oddsidemargin}{-.25in}
\setlength{\textwidth}{17cm}
\setlength{\textheight}{27cm}
\pagestyle{empty}
\begin{document}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Toto je více či méně nutná hlavička, která nastavuje základní parametry dokumentu, použité kódování textu (utf8), okraje a přidává některé speciální matematické balíčky (amsmath a amssymb). Poslední příkaz říká, že tady začíná vlastní tělo dokumentu, podobně jako např. v jazyce HTML.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\begin{center}
\textbf{4. písemná práce z~matematiky}
\end{center}\vspace{-3mm}
Jméno: \hfill Třída:\hspace*{1cm}\\[0.2cm]
\hspace*{\fill} \hspace{1cm} \textbf{A}  \hfill Datum:\hspace*{1cm}\\
\textbf{Zadání:}\\[-3mm]
\hrule\vspace{3mm}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Tohle je moje zřejmě zbytečně složitá hlavička stránky. Jednou jsem ji komplikovaně vytvořil a dál neměnil. Určitě to jde jednodušeji, ale takhle to alespoň vypadá jako tajná šifra.

Odřádkování se v LaTeXu provádí pomocí prázdného řádku, nebo k tomu můžete použít příkaz \\, za kterým může (nemusí) následovat velikost mezery zadaná nějakým způsobem, třeba v cm, mm či jinak. Povel \textbf sází tučné písmo a \hrule přidá vodorovnou čáru.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\newcounter{uloha}
\setcounter{uloha}{1}
\newcommand{\priklad}{\noindent\theuloha\stepcounter{uloha})\ }
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Jediné vylepšení, které můj dokument obsahuje a které nyní může působit zbytečným dojmem. Vytvořil jsem si nový příkaz \priklad, pomocí kterého uvozuji každý příklad a který v podstatě dělá to samé, co klasické číslování řádků. Původně měl tento příkaz trochu větší opodstatnění, nyní alespoň jeho použití zpřehlední zdrojový kód dokumentu.

Dál už následují vlastní příklady ukončené příkazem \newpage pro vložení nové stránky, na které z počátku resetuji sčítač úloh. Dál je to stejné jako na první straně.

Trocha matematiky

Matematické výrazy se píší mezi značky dolaru $ a sází se speciálním písmem. Pokud uvedete na každé straně dolary dva $$, bude vzorec vysázen na samostatný řádek. Dál si uveďme několik příkladů, které se vám mohou hodit.

Následující příklady si můžete stáhnout v samostatném souboru pokus.tex nebo prohlédnout výstup v souboru pokus.pdf.

Horní dolní index

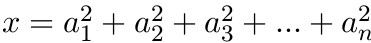$x = a_1^2 + a_2^2 + a_3^2 + \ldots + a_n^2$ $x = a_1^2 + a_2^2 + a_3^2 + \ldots + a_n^2$

$x = a_1^2 + a_2^2 + a_3^2 + \ldots + a_n^2$

Je přitom jedno, jestli napíšete a_1^2 nebo a^2_1. Mezery jsou nepovinné, LaTeX je nastavuje automaticky. Pokud je ovšem budete používat, zpřehledníte si tím čtení zdrojového souboru.

Zlomky a závorky

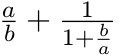$\frac{a}{b} + \frac{1}{1 + \frac{b}{a}}$ $\frac{a}{b} + \frac{1}{1 + \frac{b}{a}}$

$\frac{a}{b} + \frac{1}{1 + \frac{b}{a}}$

Vysázený zlomek je však příliš malý. I když by šlo nastavit jinak (např. pomocí \displaysize), později jsem se uchýlil k příkazu \dfrac z balíčku amsmath, který zlomky sází větší. Změna by byla následující a \dfrac i \frac je možno navzájem kombinovat.

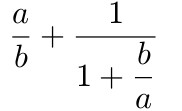$\dfrac{a}{b} + \dfrac{1}{1+\dfrac{b}{a}}$ $\dfrac{a}{b} + \dfrac{1}{1+\dfrac{b}{a}}$

$\dfrac{a}{b} + \dfrac{1}{1+\dfrac{b}{a}}$

Závorky se pak dělají klasickým způsobem. V situaci, kdy ovšem potřebujete (zpravidla kvůli zlomku) větší závorku, použijte raději příkazy \left a \right.

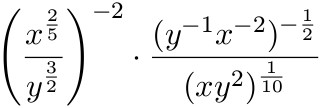$\left(\dfrac{x^\frac{2}{5}}{y^\frac{3}{2}}\right)^{-2}\cdot \dfrac{(y^{-1}x^{-2})^{-\frac{1}{2}}}{(xy^2)^\frac{1}{10}}$ $\left(\dfrac{x^\frac{2}{5}}{y^\frac{3}{2}}\right)^{-2}\cdot \dfrac{(y^{-1}x^{-2})^{-\frac{1}{2}}}{(xy^2)^\frac{1}{10}}$

$\left(\dfrac{x^\frac{2}{5}}{y^\frac{3}{2}}\right)^{-2}\cdot \dfrac{(y^{-1}x^{-2})^{-\frac{1}{2}}}{(xy^2)^\frac{1}{10}}$

Také můžete použít příkaz \big a pro ještě větší závorky \Big.

$s_x=\sqrt{{\frac{1}{n}} \big [(x_1-\overline{x})^2 + (x_2-\overline{x})^2 +\ldots + (x_n-\overline{x})^2 \big ]}$ $s_x=\sqrt{{\frac{1}{n}} \big [(x_1-\overline{x})^2 + (x_2-\overline{x})^2 +\ldots + (x_n-\overline{x})^2 \big ]}$

$s_x=\sqrt{{\frac{1}{n}} \big [(x_1-\overline{x})^2 + (x_2-\overline{x})^2 +\ldots + (x_n-\overline{x})^2 \big ]}$

Případně lze použít:

$s_x=\sqrt{{\frac{1}{n}} \Big [(x_1-\overline{x})^2 + (x_2-\overline{x})^2 +\ldots + (x_n-\overline{x})^2 \Big ]}$

Odmocniny

$\sqrt{v+5}-\sqrt{v^2-7}=0$ $\sqrt{v+5}-\sqrt{v^2-7}=0$

$\sqrt{v+5}-\sqrt{v^2-7}=0$

N-tá odmocnina se pak provádí takto:

$\sqrt[3]{v+5}-\sqrt[2]{v^2-7}=0$ $\sqrt[3]{v+5}-\sqrt[2]{v^2-7}=0$

$\sqrt[3]{v+5}-\sqrt[2]{v^2-7}=0$

Goniometrické funkce

Funkce sinus a cosinus jsou jasné, problém ovšem nastává s funkcemi tangens a cotangens. Proto ně jsem si nadefinoval vlastní nové příkazy:

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\newcommand\tg{\qopname\relax o{tg}}
\newcommand\cotg{\qopname\relax o{cotg}}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

...které dál používáme běžným způsobem.

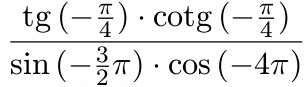$\dfrac{\tg{(-\frac{\pi}{4})} \cdot{\cotg{(-\frac{\pi}{4})}}} {\sin{(-\frac{3}{2}\pi)} \cdot \cos{(-4\pi)}}$ $\dfrac{\tg{(-\frac{\pi}{4})} \cdot{\cotg{(-\frac{\pi}{4})}}} {\sin{(-\frac{3}{2}\pi)} \cdot \cos{(-4\pi)}}$

$\dfrac{\tg{(-\frac{\pi}{4})} \cdot{\cotg{(-\frac{\pi}{4})}}} {\sin{(-\frac{3}{2}\pi)} \cdot \cos{(-4\pi)}}$

Množiny

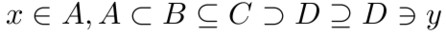$x \in A, A \subset B \subseteq C \supset D \supseteq D \ni y$ $x \in A, A \subset B \subseteq C \supset D \supseteq D \ni y$

$x \in A, A \subset B \subseteq C \supset D \supseteq D \ni y$

Pokud chcete odlišit označení množin od běžného textu, můžete k tomu také použít kaligrafické písmo, to vypadá takto:

$\mathcal{ABCD}$ $\mathcal{ABCD}$

$\mathcal{ABCD}$

Řecká abeceda

Tady platí, že pokud víte, jak se to píše, pak to bude zřejmě umět i LaTeX.

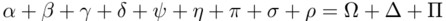$\alpha + \beta + \gamma + \delta +\psi + \eta + \pi + \sigma + \rho = \Omega + \Delta + \Pi$ $\alpha + \beta + \gamma + \delta +\psi + \eta + \pi + \sigma + \rho = \Omega + \Delta + \Pi$

$\alpha + \beta + \gamma + \delta +\psi + \eta + \pi + \sigma + \rho = \Omega + \Delta + \Pi$

Takto bych mohl pokračovat ještě dlouho, ale zatím jsem toho o moc víc nepotřeboval, a tak zájemce o další matematické symboly odkážu na vyhledávač www.google.com nebo třeba návod LaTeX v kostce - matematika a LaTeX - matematika.

Písemky se píší jaksi lépe...

Z vlastní zkušeností vím, že nejhorší jsou právě začátky a nejtěžší je k něčemu se odhodlat. Jakmile překonáte tuto první fázi, vyzkoušíte několik příkladů a začnete LaTeX používat v běžné praxi, pak možná jako já uvidíte, že se jedná o mocný nástroj, který své místo najde i v dnešní době a třeba nejen v praxi učitele matematiky a jeho přípravách písemných prací.