Linux E X P R E S

Úlohy se týkají článku Naprogramujte logickou hru v Pythonu a GTK.

Úlohy z designu

Výhody Glade a GtkBuilderu

Zadání: Zkoumejte možnosti frameworku GTK a návrháře Glade. Vylepšete grafické uživatelské rozhraní aplikace. Jaké výhody přináší vývoj v Glade/GtkBuilderu?

Uveďme namátkou pět výhod Glade:

• Glade separuje problematiku uživatelského rozhraní od vlastního programování. Díky tomu návrhář uživatelského rozhraní nemusí být programátorem, při změně uživatelského rozhraní není nutno provádět kompilaci zdrojových kódů, programátorský kód zůstává prostý rozsáhlých matoucích úseků obsahujících definici uživatelského rozhraní...

• GtkBuilder podporuje celou plejádu oblíbených jazyků. Programátorovi se tak nevnucují konkrétní vývojářské technologie.

• Toolkit GTK vyniká rozsahem funkcí. Například nabízí řešení pro nápovědu, řešení pro lokalizaci, mechanismy introspekce, řešení pro zpřístupnění pro uživatele se specifickými potřebami, oznamování událostí na sběrnici D-Bus... Na GTK navazuje platforma GNOME se svými nejrůznějšími knihovnami, které lze snadno zahrnout do GTK programu.

• Zapomeňte na licenční omezení a obdobné patálie (např. softwarové patenty). Toolkit GTK je dodáván pod svobodnou licencí GNU LGPL.

• Technologie se aktivně vylepšuje a neustále se zdokonalují.

Mohutnost Glade

Snadno se přesvědčíme, že v Glade se hravě naklikají klávesové zkratky, označení hlavního okna, panely, nástrojové lišty, přidání obrázků... Glade poskytuje vše, čeho designér moderních grafických aplikací žádá.

Standard HIG

Zadání: Pracujte na odlišném uživatelském rozhraní pro aplikaci. Svoje nápady posléze konfrontujte s doporučeními v GNOME HIG.

Dokument HIG zavádí soubor konvencí, aby si desktopové prostředí GNOME i nadále udrželo konzistenci uživatelského rozhraní. Ojediněle však GNOME nectí teze HIGu. Samotný HIG upozorňuje na potíž se vzhledem ikony souborového manažeru. Název Nautilus neodkazuje na plavidlo Verneova hrdiny kapitána Nema, nýbrž odkazuje na anglické pojmenování hlavonožce loděnky. Absenci jakékoli metonymie mezi tímto bezobratlým a souborovým manažerem shledává HIG jako nepatřičné.

U naší aplikace bychom mohli chybovat při výběru názvu. Speciálně HIG odmítá evokování násilí či politické aluze. Název „Rudí proti zeleným“ tedy neodpovídá doporučením HIG. Při dodržení zásad selského rozumu v drobné aplikaci stěží zásadně popřeme principy HIGu.

Adresář /usr/share

Zadání: Prohlédněte si obsahy některých adresářů v /usr/share. Všimněte si zdrojů souvisejících s uživatelskými rozhraními.

V adresáři /usr se shromažďují soubory pro čtení tvořící sekundární hierarchii, jež připomíná kořenový adresář /. V adresáři /usr/share jsou aplikacemi sdílená data nezávislá na architektuře. Běžně /usr/share shromažďuje například množství obrázků z uživatelských rozhraní.

Úlohy z programování

Zadání: Algoritmus nápovědy hrubou silou prohledává celý stavový prostor. Naprogramujte nápovědu, která uživateli radí nejlepší tahy. (Nejlepší tahy řeší libovolnou situaci s nejmenším možným počtem inverzí barev.) Lze v předchozím úkolu vtipně využít předností Pythonu?

Tvorba nápovědy

Ano, v úkolu lze využít předností Pythonu. Uveďme namátkou pět výhod Pythonu:

• Python exceluje bohatostí syntaxe, přičemž programátor může volit různé programátorské přístupy (paradigmata).

• Python se těší značné popularitě a většina distributorů standardního interpreta CPython předinstalovává jako součást softwarového minima.

• Python zvládne různé role. Python pohání desktopové aplikace, webové portály běží v Djangu či jiných pythoních frameworcích, Python skriptuje kód v jazyce C (rozhraní Python C API), Python funguje jako jazyk uživatelského skriptování v mnoha aplikacích...

• Python, maje zvláštní syntaxi pro nejvýznamnější referenční typy, vysoce efektivně a úsporně formuluje algoritmy. Svou stručností Python skutečně vyniká.

• Python disponuje metajazykovými prostředky, čímž dokáže snadno funkcí eval vyhodnocovat zdrojový kód, který vznikne až za běhu programu. (Kdybych níže předvedený efekt prováděl třeba v C/C++, pak by bylo nutné uložit zdrojový kód, spustit kompilátor a výsledek načíst jako sdílený objekt.)

Poslední dvě výhody v chystaném kódu blíže demonstruji. Fronta se v Pythonu zapisuje prostě jako [první_položka, druhá_položka, třetí_položka, čtvrtá_poslední_položka]. Slovník se v Pythonu zapisuje prostě jako { první_klíč:první_hodnota, druhý_klíč:druhá_hodnota, třetí_klíč:třetí_hodnota, čtvrtý_klíč:čtvrtá_hodnota}. Příkaz str vypíše definiční řetězec výrazu. Antagonistický příkaz eval definiční řetězec vyhodnotí. Složení str a eval tedy funguje jako operátor klonování. Zároveň transformací fronty na řetězec znaků získám hashovatelnou reprezentaci fronty, která může hrát funkci klíče v slovníku. Že frontu Python implementuje jako referenční nehashovatelný typ a eval(str()) realizuje klonování, ilustruje následující práce v terminálu Pythonu.

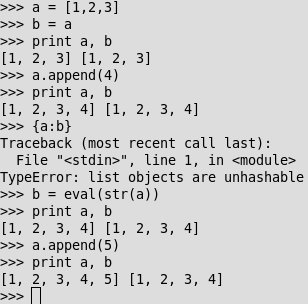Ověřování vlastností Pythonu v jeho terminálu

V ukázce proměnná a přechovává frontu. Frontu přeřadím do proměnné b a provedu její změnu skrze změnu proměnné a. Výpisem se přesvědčím, že změna proběhla též v druhé proměnné. Vytváření slovníku zkolabuje, protože fronta není hashovatelný typ. Do proměnné b naklonuji a přes fintu eval(str(a)). Nyní se přesvědčím, že změny jedné proměnné neovlivní druhou, a tudíž obě proměnné nesdílejí týž objekt.

Kód logiky tvorby nápovědy

Samotný algoritmus nápovědy se vměstnal do pouhých jedenácti řádků. Komentáře k jedenácti řádkům:

• řádek 23: Tento slovník u každé pozice uvede doporučené nastavení masky pro optimální hru. Pozice budu charakterizovat řetězcem str(barvy).

• řádek 24: Budu zpětně procházet strom do šířky a uzly ukládat do fronty nove. Inicializuji seznamem frontou s cílovým postavením. Výraz 12 * [False] elegantně zapisuje frontu dvanácti hodnot False.

• řádek 25: Procházím, dokud zbývá co k procházení...

• řádek 26: Z fronty vyjmu první hodnotu.

• řádky 27 až 30: Postupně generuji všech dvanáct pozic dostupných z aktuální pozice.

• řádek 31: Vygeneroval-li jsem dosud neznámou pozici...

• zbytek: Uložím si nastavení prvního prvku masky, což jednoznačně určí optimální tah z pozice. Aktualizuji frontu nove o nově nalezenou pozici.

Téma nápovědy dokončím hned v další otázce přidáním kódu pro vykreslování rad.

Vylepšení vykreslování

Zadání: Vyhledejte dokumentaci ke Cairo. S pomocí dalších primitiv (např. čáry) a efektů (např. průhlednost) zdokonalte vykreslování hlavolamu.

Dokumentaci Caira ukrývají oficiální stránky cairographics.org. Při plnění úlohy ukážu, jak vykreslit barevný obdélník a vysázet text do obrázku. Vylepšený program bude ukazovat uživateli optimální řešení.

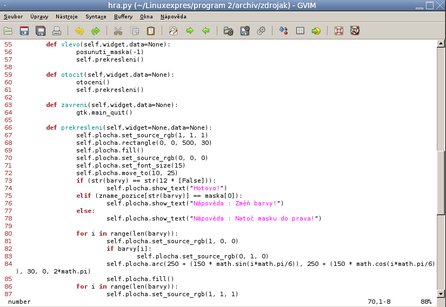Kód s logikou zobrazení nápovědy

Komentáře k novému kódu ve vykreslovací funkci:

• řádky 67 až 69: Bílou barvou vykreslím obdélník. V něm se uživateli bude dostávat rad nápovědy.

• řádky 70 až 72: Nastavím černou barvu písma, velikost fontu písma na 15 a počátek souřadnic pro renderování nápisu.

• řádky 73,74: Nápověda radí v cílové pozici Hotovo!.

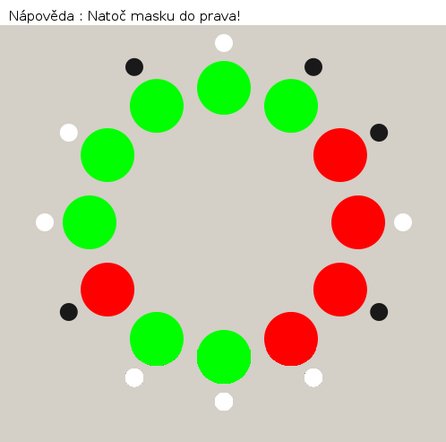
• řádky 75,76: Nápověda radí Nápověda: Otoč barvy!, je-li to optimální postup.

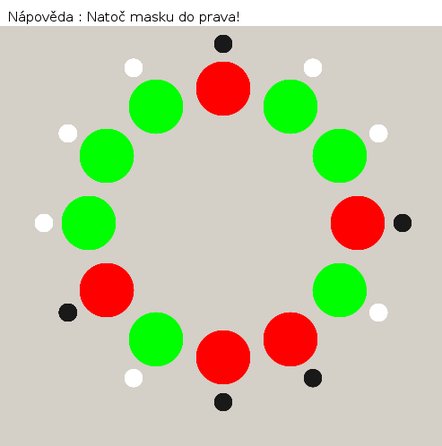
• řádky 77,78: Nápověda radí Nápověda: Natoč masku doprava!, je-li to optimální postup.

Po stažení si můžete celou nápovědu vyzkoušet. Pozor, aplikace startuje až v řádu vteřin. Řešení s řazením tisíců textových řetězců slovníkem je sice efektní, ale není výpočetně efektivní.

Nápověda doporučuje vždy otočit barvu a posunout masku o jednu pozici. Barvy se mění zdánlivě chaoticky, avšak velmi rychle se nečekaně objeví kýžený stav (podobně jako např. u Arnoldova zobrazení). Viz obrázky s finálním programem v akci.

Začátek hry

Po čtyřech tazích

Po osmi tazích

Konec hry

Náhodné simulace

Zadání: Napište program provádějící náhodné tahy. Statisticky zjišťujte, po kolika tazích program průměrně hlavolam vyřeší. Proveďte dostatek simulací, aby odchylka vašeho výsledku od skutečné hodnoty byla nejvýše 100 tahů na alespoň 99% hladině spolehlivosti.

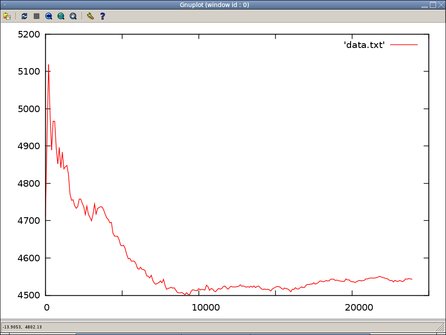
Následující kód přidaný k funkcím s logikou hry realizuje náhodné hry. Po každých sto náhodných hrách vypíše průměrnou délku hry ze všech dosud provedených simulací. Možnou evoluci průměrné délky hry v závislosti na počtu simulací jsem vynesl do následujícího grafu. K vykreslování se hodí program gnuplot, jehož stručné představení podává článek Gnuplot: Generujte grafy přímo z vašeho programu.

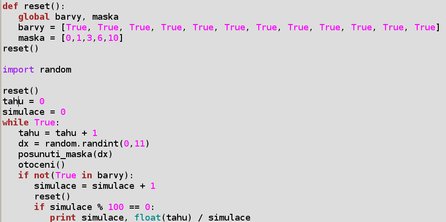Logika generování náhodných her

Vývoj průměrné hodnoty

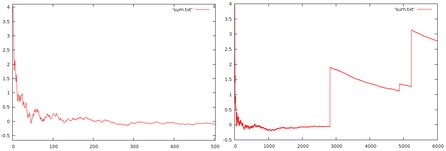
Z principu může jakákoli metodika měření v určitých situacích selhat. Příkladem jsou úlohy, kdy průměrnou hodnotu vychylují vzácné extrémní výsledky (tzv. výstřelový šum). Většinou série simulací skončí příliš brzy, poskytne nereprezentativní vzorek, a proto se nezohlední nepříliš frekventované extrémní hodnoty. To dokládají dvě zvětšení téhož fiktivního statistického souboru. Ač levý graf zdánlivě prokazatelně nasvědčuje, že průměrná hodnota je nula, pravý přesnější graf s větším časovým horizontem zahrnuje i tři extrémní hodnoty. Pravým grafem se dokonale vyvrací dojem z levého grafu.

Graf s výstřelovým šumem

Vygenerujme dostatečně velký statistický soubor; volím alespoň dvacet tisíc simulací. U tohoto čísla již mohu legitimně očekávat, že vzorek bude reprezentativní. (Jde o značně velkorysou dolní mez, poněvadž reprezentativní budou i řádově menší vzorky.)

99% hladina spolehlivosti znamená, že při 99 % spuštění programu bude odpověď v rámci tolerance správná. Možnosti ověření minimální hladiny spolehlivosti jsou:

• Datové soubory analyzovat v statistickém softwaru (např. systém R).

• Průměrný počet tahů spočítat exaktně a získat tak jistotu.

• Zvýšit počet pokusů a výsledky porovnat. Tuto metodu použiji.

Provedu osm nezávislých experimentů. Vzhledem k reprezentativnosti každého vzorku očekávám, že s 50% pravděpodobností bude výsledek získaný experimentem nižší správné hodnoty. Pravděpodobnost, že každý jeden z osmi experimentů podhodnotí výsledek, je tedy 1:256. Analogicky pravděpodobnost současného nadhodnocení je rovněž 1:256. Pravděpodobnost, že správná hodnota spadne mezi maximum a minimum z osmi experimentů, je vyšší než 99 %. Liší-li se maximum a minimum osmi experimentů méně než o 200, střed intervalu se odchyluje od správné hodnoty o méně než 100 s více než 99% pravděpodobností.

Takto jsem metodou Monte Carlo zjistil, že průměrná délka hry je 4513 tahů na alespoň 99% hladině spolehlivosti.

Matematické otázky

Zadání: Kolik pozic je dosažitelných legálními tahy z počáteční pozice? Existuje výpočetně efektivní algoritmus pro hledání nejlepších tahů v podobných hrách?

Zjevně platí, že koncová pozice nezáleží na pořadí tahů a dvojnásobná aplikace téhož tahu je identita (pozice se nezmění). Problém nalezení ideální hry se tím převádí na problém řešení dvanácti lineárních rovnic o dvanácti proměnných řešených v zbytcích po dělení dvěma. Jednou z rovnic je třeba A0 = X0 + X1 + X3 + X6 + X10 (mod 2), kde:

• Proměnná A0 je jedna, pokud má být barva na nulté pozici změněna. V opačném případě je A0 rovno nule.

• Proměnná X0 je jedna, pokud byl proveden tah spočívající v otočení barev při základním postavení masky. Nebyl-li tah proveden, je X0 rovno nule.

• Proměnná X1 je jedna, pokud byl proveden tah spočívající v otočení barev při masce posunuté ze základního postavení o jednu pozici. Nebyl-li tah proveden, je X0 rovno nule.

• Obdobným způsobem jsou zavedeny proměnné X3, X6 a X10.

Soustavu těchto jedenácti rovnic řeší známé algoritmy. Algoritmus pro hledání nejlepších tahů je třeba Gaussova eliminace. Řešení hrubou silou má exponenciální časovou složitost. Gaussova eliminace má kvadratickou časovou složitost a jde tedy o efektivní algoritmus.

V některých podobných hrách provedení sledu několika tahů může být ekvivalentní provedení jiného tahu. Řečeno vektorovou terminologií jsou tahy lineárně závislé. Úpravou matice s koeficienty soustavy rovnic se snadno zjistí, že maximální množina lineárně nezávislých tahů je v diskutované hře množina všech dvanácti tahů. Soustavu lze vyřešit při dvanácti vazbách, protože všechny tahy jsou vzájemně nezávislé. Dosažitelné je tedy dvě na dvanáctou (tj. 4096) pozic.

Zadání: Vzdáleností pozic A a B definujme minimální počet inverzí barev, který umožňuje přejít z pozice A do pozice B. Je maximální vzdálenost pozic (tzv. průměr grafu) přesně dvanáct? Jaká je průměrná vzdálenost pozic?

Dvě pozice se mohou lišit nejvíce ve 12 tazích, protože existuje pouze 12 různých tahů a žádný tah se při optimální hře neprovádí dvakrát. Definující tahy lze zvolit libovolně, a proto se v průměru dvě pozice liší v polovině tahů. Průměrná vzdálenost je tedy 6. V případě, že nejsou dosažitelné všechny pozice (tj. některé tahy jsou lineárně závislé), maximální vzdálenost a průměrná vzdálenost neexistují.

Výše uvedené úvahy nevycházejí ze specifik volby masky, počtu kroužků, počtu barev... Tudíž ideje byly de facto podány bez újmy na obecnosti a snesou přímočaré zobecnění.