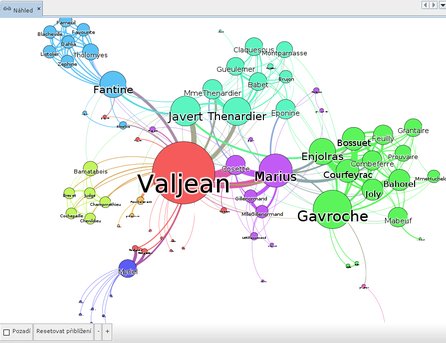
Demonstrační ukázka níže je přiložena k základní instalaci aplikace (soubor miserables.gefx). Graf zachycuje důvěrnost vztahů mezi postavami ze světa románu Bídníci. Jak okamžitě vidno, hlavní hrdinou díla je osoba Valjean. Mezi další hlavní postavy bohatě zalidněných Bídníků patří Fantine, Gavroche, Marius, Javert a Thenardier. Osoby jako Tholomyes, Dahlia, Zephine a Listolier jsou zapojeny do děje skrze Fantinu. Tato fakta jsem lehce vypozoroval z grafu, aniž bych od Victora Huga cokoliv přečetl.
V praxi se Gephi využívá v sociologii, především při výzkumu nových médií, zjišťování obsahu komunikace, v oblasti genetiky a biochemie, některých dalších oborů přírodních věd, zobrazování provozu na internetu a sociálních sítích (Neúplný soupis vědeckých článků, které obsahují grafiku z Gephiho, naleznete zde.) Zjevně se v Gephim vizualizují především data pořízená a předzpracovaná jinými aplikacemi; Gephi nezajišťuje samotný sběr dat a zpracování dat zajišťuje jen na té nejzákladnější úrovni.
Gephi lze nasadit nejlépe tam, kde se ukládá v unifikované podobě velké množství poznatků. Poznatky, ač jednotlivě mají nepatrnou vypovídací hodnotu, jako celek nabudou značné vypovídací hodnoty. Zobrazované údaje by měly být rozložitelné na vztahy mezi dvojicemi objektů.
O těchto strukturách pojednává teorie grafů, s níž se shoduje terminologie uživatelského rozhraní Gephiho. V teorii grafů se objekty označují jako uzly nebo u některých autorů jako vrcholy, vztahy mezi objekty se nazývají hrany. Intenzita vztahu se označuje jako váha hrany. Data, která nelze takto chápat (např. vztahy mezi trojicemi objektů), nelze v Gephim zobrazit.
Rozložení uzlů
Vysvětleme terminologii na konkrétním příkladu tenisových hráčů. Tenisté se zobrazí jako uzly a vztahy mezi nimi jako hrany. Hrany jsou neorientované, nebo orientované. Neorientovaná hrana, u níž nezáleží na pořadí hráčů, představuje událost, že vloni dva tenisté hráli vzájemný zápas.
Orientovaná hrana zohledňuje událost, že vloni první tenista alespoň jednou porazil druhého tenistu. Hraně může být přiřazena váha. Vahou může být počet loňských zápasů, důležitost zápasu (exhibice, finále, první kolo...), zda se odehrál zápas nedávno nebo finanční dotace turnaje.
Hráči Tomáš Berdych a Novak Djokovič se pravděpodobně střetnou, protože vzájemně souvisejí svou mimořádnou výkonností. Dva kluboví hráči z téhož města se pravděpodobně také utkají, protože vzájemně souvisejí blízkostí bydliště. U amatérských hráčů záleží hlavně na bydlišti. Amatérské hráče je tedy přirozené zobrazovat do mapy podle bydliště, ale u profesionálních hráčů se bydliště stává nepodstatným. Gephi proto nabízí několikero principů, jak umisťovat uzly do zobrazovací plochy.
- Uzly se mohou rozházet po ploše náhodně, což nemá valnou vypovídací hodnotu.
- U místně lokalizovaných dat umístění uzlu odpovídá zeměpisnému místu, kde se daný jev nachází. Každému uzlu musí být přiřazeny správné geografické souřadnice. Ty určují bod na sféře, nikoliv v rovině, proto při zobrazování jevů rozsáhlejších oblastí (např. Rusko) nutno případně vybrat kartografickou projekci.
- Někdy záleží na pořadí dat. Uzly jsou nějak uspořádány do posloupnosti či posloupností, například podle pozice v datovém souboru. Následně jsou uzly od prvního po poslední vykresleny třeba po obvodu kruhu. Takto bychom vykreslili tenistky první stovky.
- Konečně Gephi zná uspořádání podle "vnitřních souvislostí" uzlů.
A právě uspořádání podle "vnitřních souvislostí", jež udávají hrany mezi uzly a upřesňují váhy hran, se hodí pro nejvíce situací. Uživatel požaduje, aby vzájemně související objekty, to jest uzly spojené hranami, ležely blízko sobě a aby vzájemně nesouvisející objekty neležely blízko sobě. Takto se v ukázkovém grafu vytvořilo několik shluků uzlů, například již zmínění Fantinini blízcí. Shluky uzlů (clustery) tvoří podmnožiny uzlů takové, že z clusteru vystupuje málo hran a současně uvnitř clusteru existuje mnoho hran.
U složitějších grafů brání topologická omezení daná dvojrozměrnou plochou, na níž zobrazujeme dosažení optimálních výsledků tak, aby se vždy respektovaly podmínky na blízkost souvisejících uzlů a neblízkost nesouvisejících uzlů. Východiskem je zobrazování do mnoharozměrného prostoru, což v praxi není možné, anebo vhodné přibližné řešení. Navíc nalezení optimálního rozložení je příliš výpočetně náročné, jelikož se jedná o NP-úplnou úlohu.
Předpřipravené aproximační algoritmy pro výpočet rozložení převádějí problém nalezení vhodného rozložení uzlů na řešení fyzikální soustavy hmotných bodů. Hmotné body (uzly) spojené hranou se vzájemně přitahují. Čím větší váha hrany bude, tím intenzivnější síly budou působit. Kolapsu soustavy do "těžiště" brání odpudivé síly.
Dostředivé síly převažují v clusterech, tudíž v clusterech se zvyšuje hustota uzlů, potažmo snižují se vzdálenosti mezi uzly. Naopak vně clusterů převládají odpudivé síly. Algoritmy v Gephim evoluci systému numericky modelují, přičemž disipují volnou energii. Jak energie ubývá, systém se blíží stabilnímu stavu.
Na počátku simulace jsou uzly rozmístěny nahodile.

Rozložení se po každé iteraci překresluje do panelu graf. Uživatel může průběžně sledovat, jak rozložení spěje ke konečnému výsledku. Obvykle po několika vteřinách se uzly uspořádají. Konvergence se zpomaluje.
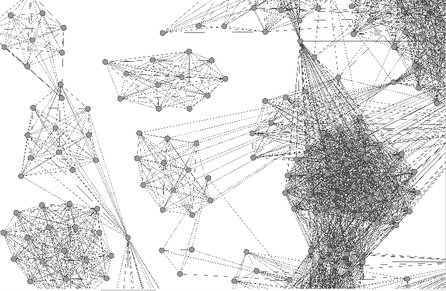
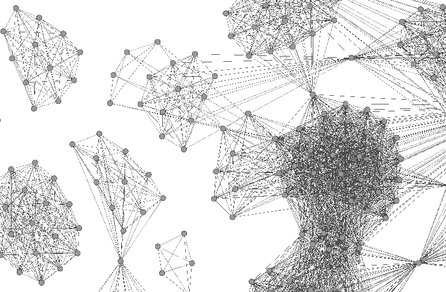
Konvergence se může dočasně zrychlit, když se systém ve fázovém prostoru vzdálí od inflexu. Nakonec se systém ale přece jen zákonitě ustálí.
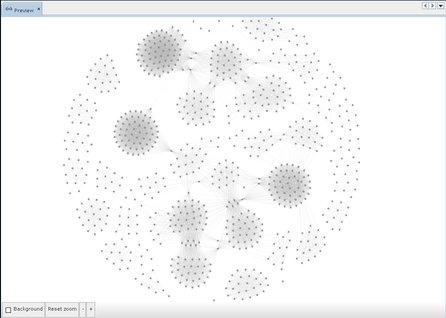
V ideálním případě simulovaný systém dospěje ke globálnímu optimu. Uvíznutí mimo globální minimum je možné, ba pravděpodobné, poněvadž u komplikovaných grafů existuje mnoho lokálních minim. Někdy konečné rozložení může být zjevně suboptimální.
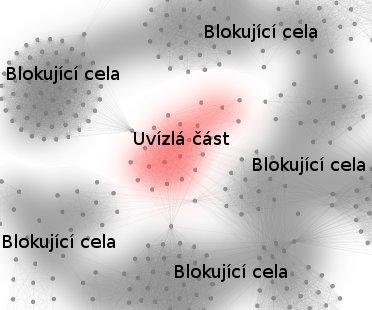
A zrovna u předchozího grafu zabraňuje bariéra z clusterů okolo středu úniku uzlů ze středu, a tak simulace nikdy nenalezne optimum. Navíc nepatrná změna v datech u předchozího grafu nezřídka vyvolá značnou změnu v konečném rozložení (chaotické chování algoritmu). Problémy se překonají, když:
- Použije se "nefyzikálního" algoritmu. Tyto algoritmy však v základní instalaci chybí.
- Změní se algoritmy nebo jejich parametry tak, aby se celistvá bariéra roztrhala.
Gephi nabízí v základní instalaci několik "fyzikálních" algoritmů, které se liší v použitém fyzikálním modelu, paměťových nárocích, rychlosti výpočtu, schopnosti rozkládat zatížení u SMP a rychlosti konvergence. Chování algoritmů lze doladit nastavením parametrů, jež definují průběh působících sil v závislosti na vzdálenosti.
Vysvětlení parametrů však chybí (viz sekce Nedostatky). U algoritmů se rovněž neuvádí, zda jsou výpočty numericky stabilní. Jinými slovy mohou dva počítače u stejných dat dospět k rozdílným rozložením jen kvůli tomu, že různý hardware počítá s různou přesností a jinak zaokrouhluje? Toto bude uživatele zajímat, vyžaduje-li maximální reprodukovatelnost výsledků (U Javy, na níž běží Gephi, se opakovatelnost výpočtu zajišťuje deklarací strictfp.)
Grafická prezentace
Po získání rozložení je třeba ještě nastavit barvy, font písma a různé další úpravy konečného vzhledu, tak se zajistí, že výsledný graf seznamuje například s jmény a národnostmi tenistů. Někdy je nutné dále i zvýraznit sousedy určitého uzlu... O těchto praktických tématech bude pojednávat až další díl článku.
Lokalizace do češtiny
Vedle angličtiny, ruštiny a několika dalších jazyků je Gephi z větší části lokalizováno i do češtiny. Částečný český překlad však někdy nerespektuje vžitou odbornou terminologii. Například "undirected edge" se otrocky překládá jako neřízená hrana, nikoliv správně jako neorientovaná hrana. Na některých místech český překlad zní kostrbatě, což dále snižuje jeho srozumitelnost. Celkově při porovnání s ostatním matematickým softwarem se zdejší čeština jeví jako průměrná.
Nedostatky
Bohužel chybí jakákoliv nápověda, což mnohdy znemožňuje účinně Gephi využívat. Například si zvolíte algoritmus pro výpočet rozložení. U algoritmu naleznete, řekněme, deset nastavitelných parametrů. Tovární nastavení parametrů vám nevyhovuje, tak si chcete parametry přenastavit. Z krátkých popisků však nepochopíte, co ten který parametr přesně ovlivňuje.
Navíc vám chybí byť jen řádová představa o obvyklých hodnotách parametrů. Nevíte, zda u toho kterého parametru zkoušet hodnoty v řádu tisíců nebo jednotek. Zkrátka metodou pokus-omyl se jen obtížně dosahuje kýženého výsledku. Bohatě by stačil krátký vysvětlující odstavec.
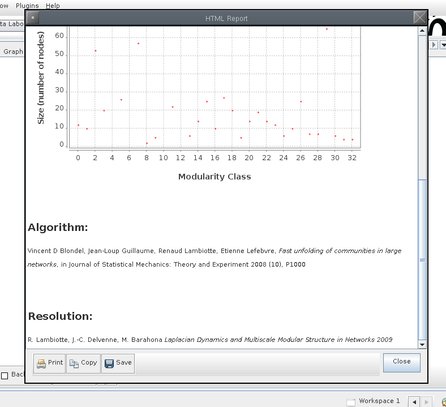
Gephi nic zásadně nevysvětluje, vždy jen odcituje článek z vědeckých časopisů, jenž popisuje příslušný algoritmus. To je jistě chvályhodné, leč vcelku zbytečné. Pochybuji, že běžný uživatel si bude citované články obstarávat. Pokud si přece jen článek obstará, možná při čtení pochopí pouze to, že v angličtině nerozumí odborné anglické terminologii.
Čeho se týká graf na obrázku, se dozvíte jen ze článku Fast ufolding of communities in large networks a článku Laplacian dynamics and multiscale modular structure in networks. Podobně zamlžená je většina hlášení z panelu Statistika.
Dále uživatelské rozhraní rozhodně není dodělané a odladěné. Rozhraní je i nedomyšlené. Například uložíte projekt a hned kliknu, abych zavřel Gephi, načež se Gephi nesmyslně ptá, zda chcete změny uložit. I po zamítnutí některé možnosti zůstanou upřesňující parametry nastavitelné. Uživatelé tudíž mohou nastavovat parametry neaktivních funkcí, přičemž se zmateně diví, proč aplikace na změny nereaguje. Nezkušený uživatel snadno ztratí povědomí, co vlastně dělá.
Především je však uživatelské rozhraní silně zabuggované. Při zpracovávání ukázkového grafu jsem se setkal mimo jiné s následujícími chybami. Poklepání na tlačítko překreslování grafu ne vždy opravdu způsobí překreslení grafu. Při přibližování překresleného grafu někdy zmizí všechny hrany. Dialog se špatně překresloval, což vyřešil pouze restart celé aplikace.
Při rutinních úkonech se člověk snadno dopustí chyby, aniž si nedopatření vůbec uvědomil, a plýtvat lidskou práci na rutinní úkoly není ani efektivní. Bohužel v Gephi absentuje silný skriptovací nástroj a nahrávání maker, což by zautomatizovalo monotónní činnosti. Postrádám i funkci pro vracení změn.
Shrnutí
Stále levně lze získávat stále rozsáhlejší a stále reprezentativnější soubory dat, což způsobuje technický pokrok, elektronizace společnosti, globalizace, standardizace, monopolizace internetu a změna postojů veřejnosti k problematice ochrany soukromí. S větší dostupností se zvyšuje potřeba nadbytek dat shrnout do přehledné vizuální formy, nikoliv jen vypsat v textové podobě. Na zobrazení dat, která lze chápat jako sítě, se specializují především aplikace Gephi a Tulip.
V Gephim si lze graf snadno naklikat s důrazem na hezkou vizuální prezentaci. Pro toto zaměření Gephiho autoři přirovnávají svůj produkt ke grafickému editoru Photoshopu. Gephi je malá graficky orientovaná aplikace s přehledným nekomplikovaným uživatelským rozhraním, které není třeba se dlouze učit. Intuitivnosti se však dosáhlo na úkor rozsahu funkcí. Aplikace postrádá pokročilé statistické funkce k přípravě surových dat před vlastní vizualizací. Rozsah funkcionality (např. nové algoritmy výpočtu rozložení) lze rozšiřovat nahráváním pluginů.
Hlubší analýzu statistických dat usnadňují také dataminingové aplikace (např. Orange) a velký statistický software. V oblasti složitější statistiky je zřejmě nejpoužívanějším nástrojem prostředí R. Tyto aplikace lze využít v součinnosti s Gephi; vhodnými aplikacemi (Orange, R, Knime, Weka, NetMiner, RapidMiner...) se surová data zpracují, extrahují se statisticky významné vztahy a ty se na závěr v Gephim jen vizualizují.
Gephi je duálně licencován licencí CDDL a licencí GNU/GPL verze 3.0. Rozdíly oproti běžnější verzi GNU/GPL verze 2.1 nejsou z hlediska běžného uživatele podstatné. Aplikace nevyžaduje instalaci. Webové stránky projektu v současnosti nabízejí stažení nejnovější beta verze 0.8.2-beta. Žádná ze starších verzí není vedena jako stabilní.
Gephi je postaveno na javovské platformě NetBeans. NetBeans primárně vzniklo jako vývojářské prostředí pro programátory, později začalo být využíváno mnoha dalšími způsoby. Ostatně podobně se začal tematicky rozšiřovat i konkurenční javovský projekt Eclipse. Gephi se pyšní dobrou kompatibilitou a podporou různých formátů.
Především je dostupné množství databázových konektorů, a tak lze snadno do Gephiho importovat data z nejrůznějších databází a tabulek kancelářských tabulkových procesorů. Například můžete vizualizovat data importovaná z online databáze MySQL od instalace softwaru Piwik, kterým jsou na LAMP serveru zaznamenány údaje o návštěvách webových stránek.
Celkově se jedná o užitečný a zajímavý, leč nedotažený, software. Jinak hodnotnou aplikaci sráží nízká kvalita provedení.
Obsah druhého dílu
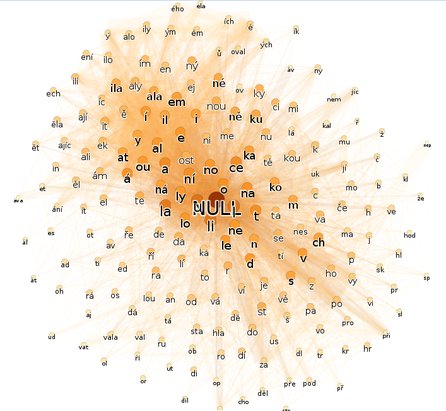
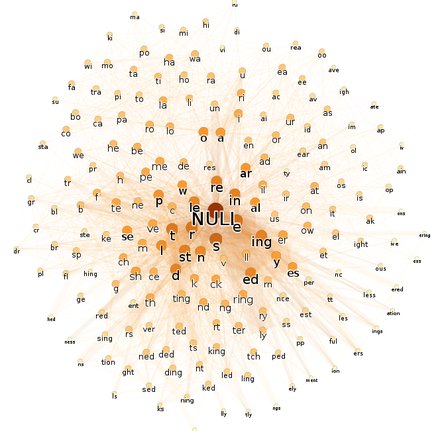
Druhý díl na konkrétním příkladě rozebere pořízení dat a jejich vizualizaci, podobným stylem jako v dřívějším článku Gnuplot: generujte grafy přímo z vašeho programu. Ukázka předvede, jak lze analyzovat volně dostupné texty v neznámém jazyce. Kraťoučkým skriptem v Pythonu (pod padesát řádků zdrojového kódu) budeme analyzovat text pomocí relace "býti podřetězcem". Skript bude vyhledávat dvojice skupin znaků vykazujících nad textem jisté chování.
Vyhledané mimořádnosti jsou u náhodných posloupností znaků krajně nepravděpodobné, tedy u nalezených skupin znaků lze rozumně předpokládat gramatický nebo slovotvorný význam. Budu takto porovnávat text v češtině, jež patří mezi nejflektivnější indoevropské jazyky, s textem v angličtině, jež patří mezi nejanalytičtější indoevropské jazyky, a výstup skriptu bude vizualizován Gephim.
Studovanými texty budou povídka Babička Boženy Němcové a Dobrodružství Toma Sawyera, významné dílo amerického spisovatele Marka Twaina. Délka obou textů se pohybuje okolo dvou set normostran, v obou se zhusta nalézají prvky nářečí, oba texty jsou vyprávění a podobají se i v mnohém dalším. Přes tyto shody se výsledné grafy zcela liší.
Graf vytvořený z anglického textu, jenž je již od pohledu tím řidším, správně naznačuje, že je anglický text v porovnání s českým chudší na ohýbání a odvozování slov.
![]()
![]()